ALU 만들고 FPGA에 Implement하기
논리설계 과제로 ALU(Arithmetic and logical unit)을 Verilog code로 구현하고 FPGA 보드에 Implement해 보았다.
ALU : Control(Operation) Input으로 AND, OR, XOR, ADD와 같은 논리연산의 종류를 정하고, 각 Input에 따른 결과값을 구하는 조합 논리 회로이다.
FPGA : Field programmable gate array, 설계 가능한 논리 소자와 프로그래밍이 가능한 내부 회로가 포함된 반도체 소자 - 라고 정의되어 있다. 논리값에서 새로운 논리값을 얻는 것을 논리연산이라 하고, 논리연산의 기본이 되는 소자를 논리소자(logic element)라 한다. AND, OR소자 등이 대표적이다. FPGA는 프로그래밍이 가능한 비메모리 반도체의 일종으로, 프로그래밍이 가능한 내부 회로이기 때문에, 논리 소자도 원하는 대로 새겨넣을 수 있기 때문에 유연성, 소량생산에 유리하다는 특징을 가진다.
https://www.scienceall.com/논리-소자logic-element/
이번에는 아래와 같이 FPGA로 제작된 Logic Design Board를 사용했다.

I/O ports, 6개의 아웃풋 LED, Dip및 tactile 스위치, Osicillator를 가지고 있는 것을 확인할 수 있다.
먼저 Xilinx ISE를 이용해서 ALU Module을 구현했다.
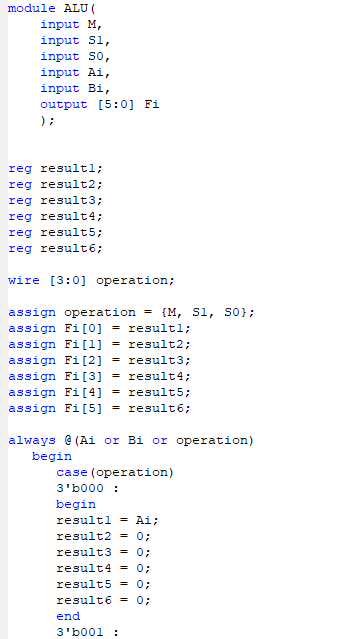
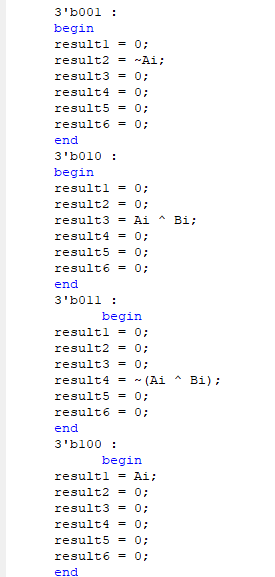
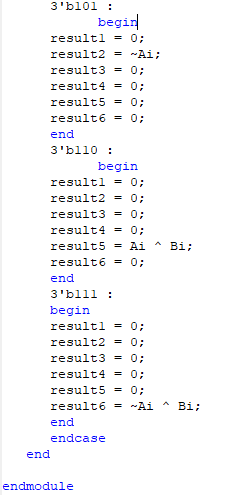
M, S1, S0로 3개 1bit 인풋을 받아서 Logic을 control해야했기 때문에, Behavioral 방식으로 구현했다. 로직을 선택할 때마다 이전 값이 남아있으면 안되기 때문에 6개의 register를 이용했는데, 이렇게 하나씩 초기화하는 방법이 맞는 방법인지는 잘 모르겠다.

ALU의 시뮬레이팅 결과이다. M, S1, S0가 컨트롤 input으로 사용되었고, Fi[0] ~ Fi[5]까지 output이 제대로 출력되는 것을 볼 수 있다.
이후 I/O pins를 Module에 연결해준 다음, Configure Target Device 기능을 이용해 iMPACT 파일을 생성하여 보드와 연결했다. DIP Switch의 작동에 따라 32가지 output이 잘 나타났다.
정렬 알고리즘(백준 2751번)
간단한 정렬 문제를 풀었다. N개의 중복이 없는 자연수를 오름차순 정렬하는 문제였는데, 처음에 시간 초과가 나와서 당황했다.
https://www.acmicpc.net/problem/2751
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
Collection.sort를 이용하여 arrayList를 정렬하고, 하나씩 println해주는 방법을 사용했다가, 이후 StringBuilder를 사용하니 시간초과가 나지 않고 통과되었다. 이후 구글링을 해보니 이러한 정렬 관련 문제는 최악의 시간 복잡도를 유도하는 testCase를 끼워넣는 경우가 있다고 한다. 내 경우에는 sb의 사용이 유의미한 차이를 냈지만, 보통 Arrays.sort를 사용하여 시간초과가 나는 경우가 많다고 한다.
지금은 PS를 공부하는 초기 단계이기 때문에 유형별로 많은 문제를 풀어보고 어떤 식의 문제가 나오는지 파악하는 것이 우선이라고 생각한다. 정렬에서 시간복잡도를 유의미하게 생각해야 한다는 것을 깨달은 것만으로도 나름의 수확인 것 같다.
마침 자료구조 수업에서 정렬 파트를 배웠는데, 시간복잡도가 굉장히 중요하게 다루어져서 공부했던게 이 문제를 풀고 난 이후 정렬 문제를 공부하고 이해하는데에 도움이 되었다.
https://st-lab.tistory.com/106
[백준] 2751번 : 수 정렬하기 2 - JAVA [자바]
www.acmicpc.net/problem/2751 2751번: 수 정렬하기 2 첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 숫자가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이..
st-lab.tistory.com
Collections.sort()는 Timsort를 사용한다고 하는데, 삽입 정렬과 병합 정렬의 알고리즘을 사용하는 hybrid sorting algorithm이라고 한다. 삽입 정렬의 경우 최악의 경우 O(n2), 최선의 경우 O(nlogn)을 보장하고 병합 정렬의 경우 최선, 최악의 경우 모두 O(nlogn)을 보장하는 것까지는 알고 있었지만, 내부적으로 두 개의 정렬 알고리즘을 혼합하여 사용한다는 점은 모르고 있었다.
https://d2.naver.com/helloworld/0315536
https://yabmoons.tistory.com/250
[ 정렬 ] 정렬별 장단점 및 시간복잡도
이번 글에서는 정렬별 장단점 및 시간복잡도를 비교함으로써 어떤 정렬이 제일 좋고 나쁜지를 알아보자 ! 사실 이 정렬법이 무조건 제일 좋아요 ! 라고 말할 수 있는 정렬법은 없다. 왜냐하면 각
yabmoons.tistory.com
수업 시간에 병합 정렬이 in-place 알고리즘이 아니고 데이터가 커질 경우 메모리를 많이 요구하며 배열 간의 정보를 옮기는 과정에서 비효율이 발생한다고 배웠는데, 이를 두 배열을 재사용하여 반복적으로 교대해줘서 효율을 증가시키는 예제가 있었다.
그런데 TimSort에서는 효율을 개선하기 위한 다른 방법으로, 참조지역성의 원리를 만족시키기 위해 병합 정렬에 삽입 정렬을 결합했다고 하는데, 참조 지역성이 왜 속도에서 중요한지는 알겠지만, 삽입 정렬을 추가하여 이를 최적화시키는 과정에 대해서는 아직 정확히 이해하지 못했다. 추후에 시간이 많으면 다시 공부해야겠다. 또, 정렬 알고리즘 별로 최적화시키는 방법에 대한 정보가 많이 있는 것 같다. 이런 것들을 공부해두면 알고리즘적 사고에 도움이 될 것 같기에 날을 잡고 공부를 해봐야겠다.
이산수학(Function, Counting, Algebras)
*Function
Domain : 정의역
Codomain : 공역
Image와 pre-image
Range : 치역
Injection : 단사 함수, 정의역 원소 하나에 공역 원소 하나가 대응되는 것
Surjection : 전사 함수, 모든 공역 원소에 대해 pre-Image가 존재하는 것. 즉, 공역과 치역이 동일
bijection : 전단사 함수, 정의역 원소 하나에 공역 원소 하나가 대응되고, 공역과 치역이 동일. 정의역과 공역 원소 수가 동일하다.
*Counting
Pigeonhole Principle : A와 B가 유한집합일 때, A의 원소 수가 B의 원소 수보다 크면 A로부터 B로 가는 Injection이 존재하지 않는다. 즉, 적어도 두개의 원소는 같은 원소에 대응된다.
Permutation / Combination / Combination with Repetition : 순열, 조합, 중복조합 - 순서를 고려하여 나열, 순서 없이 뽑기, 중복 포함 뽑기.
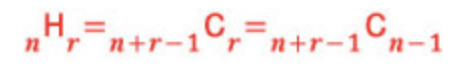
Countable / Uncountable Set : 자연수 집합 N의 자연수들과 A에 대한 bijection이 존재한다면 이 집합은 countable하다.
유리수 집합은 가산집합인가? : 좌표평면에 유리수 정의를 이용하여 자연수로 대응해주기.
Recurrence relation : 점화식 - 수열에 대한 점화식은 n번째 항이 그 전의 항(들)과 갖는 관계에 대한 등식.
점화식의 해는 Iteration 또는 linear homogeneous recurrence relations with constant coefficients(상수 계수 선형 동차 점화식)에 대한 특별한 해법으로 구할 수 있다.
*Algebras
abstract algebra에서, 대수 구조(algebraic structure)은 집합 A에 대한 operation의 collection이다. 여기서 A는 carrier라고 불리고, Operators가 정의되며, 대수의 constants라 불리는 특별한 원소들이 정의된다.
Subalgebra : 대수의 부분집합. carrier, operation의 결과, constants들이 특정 algebra에 포함되면 subalgebra라고 한다.
항등원, 역원 : 특정 operator에 대해 연산 결과가 피연산자와 같게 만드는 constants를 항등원, 항등원을 결과로 만들면 역원이라고 한다.
Semigroup : binary operation에 대해 결합법칙이 성립하면 semigroup이다.
Monoid : semigroup에서 항등원이 존재하면 monoid이다.
Group : monoid에서 unary operaotor를 통한 inverse가 존재하면 group이다.
Homomorphism : 특정 function이 operator를 통한 분리, 항등원 대입시 항등원, uanry 연산 시 unaryF()를 만족시키면 homomorphism이다.
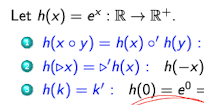
Isomorphism : homomorphism이면서 bijection이면 isomorphism이다.
느낀점
고등학교 때 배운 것들이 너무 기억이 나지 않는다... 수학의 다른 분야는 몰라도 이산수학은 다시 각잡고 공부를 해야할 것 같다. 컴퓨팅적 사고에 도움이 될만한 부분들 또는 PS에 도움이 될 부분들이 분명히 있다고 생각되기에 차근차근 다시 공부해보자...
'TIL' 카테고리의 다른 글
| [TID] #5 - UseCase와 Interface Provider / Repository Pattern (0) | 2022.10.25 |
|---|---|
| [TID] #4 - Tuist, Bundle, 동적/정적 라이브러리 (2) | 2022.10.19 |
| [TID] #3 - 나는 오늘도 개발한다? 내가 오늘 개발한 것? (1) | 2022.10.18 |
| [TIL] #1 - 스택으로 Infix to Postfix 계산기 만들기(Java) (0) | 2022.04.29 |
| [TIL] #0 - Today I Learned (2) | 2022.04.28 |

